We typically get a few questions each year about our failure rate. I’m never quite sure why people ask, or what they are expecting. Do they want to hear that the failure rate is high, so they are convinced it’s a tough (and therefore good) program? Or maybe they don’t want the failure rate to be high, because they are concerned that they won’t be successful? I’m not sure what the motivation for the question is, but anyways let’s examine failure rates.
First, a philosophical question. What is failure? We can’t measure a failure rate until the term is defined. So, is it failure if:
- you pass all your courses and the term, but decide that Engineering is not your passion and transfer to Arts?
- you pass the term (which requires a 60% average at Waterloo), but fail a course (i.e. get a grade <50%) and have to repeat that course in the future?
- you fail the term with an average between 50 and 60%, but repeat the term and go on to graduate successfully a year later than originally planned?
- you fail out of Engineering (term average <50%), but transfer and graduate from Science, Mathematics, or Applied Health Studies?
- you fail and leave Waterloo, but do very well in a college engineering technology program?
What some people might call failure, others would view as part of the learning process and finding your place in the world.
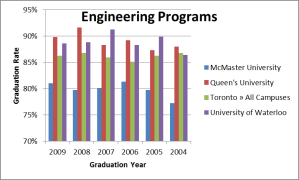
There is actually no universal definition of failure, so answering the question “what is your failure rate” is actually quite complicated. One public information source, CUDO, has a nice engine that allows you to download spreadsheets of data. They give graduation rates (sort of the inverse of failure rates), so let’s look at those. Here’s a graphical version of some graduation rate data I downloaded for engineering at Waterloo, McMaster, Queen’s and Toronto.
As the graph shows, graduation rates fluctuate between the high 70s and low 90s among these universities. It looks like you are pretty likely to graduate, so does that imply you are unlikely to fail? You have to read the fine print for the CUDO data however (as you should always do with any data). The CUDO data is based on counting the fraction of students entering engineering, who graduated from that university with any degree, within seven years. So it’s quite a bit more complicated than it looks at first glance. If some student entered engineering in 2002, failed several times and had to repeat a couple of years, switched programs and received a Bachelor of Arts in English in 2009, that would appear as a successful graduation in this CUDO data. When applicants ask “what is your failure rate”, I don’t think they have this type of scenario in mind!
If you want to know how many people start and successfully finish in an engineering program, that’s a bit more difficult. Waterloo publishes such information in annual performance reports, like the ones listed here. The 2012 report (on page 40) shows that 71% of students that started in Engineering in 2005 had graduated by 2012, 6% had received degrees in other faculties at Waterloo, 6% were still working on their degree, and 17% had left Waterloo (destination unknown). So the majority of the students that start in Engineering will finish.
Finding similar information from other universities is not easy. Toronto’s Engineering produces a nice annual report (here), but it doesn’t include the same graduation rate information. Perhaps the information exists for the other universities, but I haven’t been able to find it (admittedly I haven’t looked that hard). However, looking at other data such as 1st year registration and number of graduates suggests that the other universities have statistics that are not much different from Waterloo’s.
Finally, how does Engineering compare with other programs? We all know that engineering is a tough program, so should we expect the graduation rates to be higher in Science or Business or Arts? To check this we can use the CUDO data for 2012 again, and let’s pick one university (Toronto) to eliminate inter-university differences so we can compare programs more rigorously. Here are the reported graduation rates for a few programs:
- Business & Commerce 83.7%
- Engineering 86.2%
- Humanities 77.2%
- Mathematics 90.5%
- Nursing 97.7%
- Physical Science 85.7%
- Theology 73.9%
So, judging by graduation rates Theology and Humanities are the “toughest” programs and Nursing is easy. Or, maybe this whole failure/graduation rate thing is not particularly useful or informative for making decisions about what to do with your academic future? I suspect that being motivated and having a passion for your field will make a much bigger difference to your future than the institution’s failure (or graduation) rate statistics.
Nice article. My biggest fear is to be asked to repeat or leave the university. Can’t wait to graduate!
Thanks. Nobody wants to repeat a term, but often it can be very helpful in setting a student on a better path for success.
Failing someone because he or she didn’t know the majority of what was in the test is not a valid way to find out whether the student knows what’s going on in class. Professors and TA’s and even teachers have a checklist they use while grading and if the answer you put down isn’t what’s in the checklist, then you get an X. People find ways around this, like cheating. I know someone who has only studied for 5 courses out of the whole 5 year program and that person graduated with a high 70s average. I really think the worlds education system is flawed. Assignments, quizzes, tests etc.. Is not flawed but the dependency to pass on these is 100% flawed. If the professor remains with the class for longer than just 4 months and takes the time to know how much each student knows and is capable of, that would be a good solution, but the professor might not like the student and so, decides to fail the student instead so there is fault in that. I personally, am a bad test taker. I really love the major I’m studying, civil engineering, and I study my butt off, but when it comes to tests, I always miss a few concepts that are the main focus of a midterm or final and I end up winging it to get a 70. There really is no problem whatsoever about that. But basing my right to pass or fail a course because of a couple of mistakes is not justified at all. I apologize if I sounded rude or if you took offense to anything I said professor.
Assessing knowledge is something we struggle with, for many of the reasons you mention. No doubt it is a flawed system, but there don’t seem to be very many alternatives that would be affordable and generally accepted.
May I also add, that engineering is more than just your fulfillment of higher needs in terms of educating your mind and being exposed to ideas. Most and foremost engineering is a profession. “Missing a couple concepts here and there” in reality is not an option if you ask anyone who does engineering work professionally. Getting a 90 does not cut it. You can’t make an engine installation plan only good to 90%. It has to be 100% right or else its a fail.
While we all feel that there should be more individual assessment in class, more leeway and less weight on exams and that marking seems like a machine process there is a fundamental reason Engineering is “cut straight” the way it is. Accredited engineering programs are highly scrutinized and the concepts and methods mentioned in class are requirements (if you so will set by the public) such that people can trust your work. Still there are checks in place as everyone makes mistakes, but a lot of engineering has safety of people involved and its just to risky to have someone there designing a bridge who has a good idea and is a good learner, but cannot find the maximum in plane stress in an open section beam. Other example engineer that forgot to account for icing on one of Vancouvers bridges.
There should be a continuous learning/feedback process for generation and reception of ideas of how to improve the assessment system.
While it is reasonable to believe we won’t find perfection, complacency ought not be allowed to linger and grown in a culture of excellence.
How does the University promote and gather ideas systemically? Would a universal email address such as “ideas@[university/department.ca]waterlooengineering.ca” help?
Part of the engineering accreditation requirements now include what would be called “continuous quality improvement” in industry. So we use a variety of feedback mechanisms to assess learning and outcomes.
Pingback: Graduation Rates Revisited | A Professor in Waterloo Engineering